Functions

CSE 16: Applied Discrete Mathematics

Instructor: Owen Arden

Winter 2023

Functions? Seriously?

You know the drill by now: we are formalizing the definition and properties of functions so we can use their properties in rigorous proofs.

Topics:
- Definiton of function
- Injection, surjecition, bijection
- Inverse function
- Composition
- Floor, ceiling, factorial

Functions

Function: Let \(A\) and \(B\) be nonempty sets. A function \(f\) from \(A\) to \(B\), written \(f: A \to B\), is an assignment of each element of \(A\) to exactly one element of \(B\).; We write \(f(a) = b\) if \(b\) is the unique element of \(B\) assigned by \(f\) to the element \(a\) of \(A\).

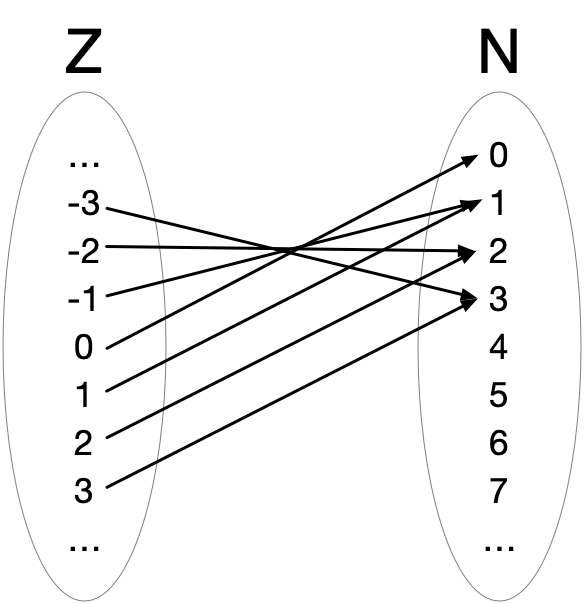
Functions are also called mappings or transformations.

Functions as relations

A funciton \(f : A \to B\) can also be defined as a subset of \(A \times B\) where no two elements of the relation have the same first element.

Formally, a function \(f\) from \(A\) to \(B\) contains one and only one ordered pair \((a, b)\) for every element \(a \in A\). \[ \forall x.(x \in A \to \exists y. (y \in B \wedge (x,y) \in f)) \]
“… and only one” \[ \forall x, y_1, y_2.((x,y_1) \in f \wedge (x, y_2) \in f) \to y_1 = y_2\]

(Co)domains and (pre)images

Given a function \(f: A \to B\):

We say \(f\) maps \(A\) to \(B\) or \(f\) is a mapping from \(A\) to \(B\).
\(A\) is called the domain of \(f\).
\(B\) is called the codomain of \(f\).
If \(f(a) = b\)
- \(b\) is called the image of \(a\) under \(f\).
- \(a\) is called the preimage of \(b\) with respect to \(f\).
Two functions are equal when they have the same domain, the same codomain, and map each elementR of the domain to the same element of the codomain.

Representing functions

Just like the different notations for defining functions, functions can be specified in different ways.

An explicit statement of the assignments
- e.g., as a relation or diagram
A formula
- \(f(x) = x + 1\)
A computer program
- A python program that, given an integer \(n\), produces the \(n^{th}\) Fibonacci number.

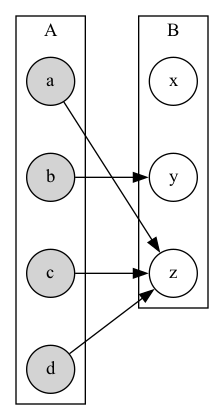
Questions

\(f(a) = ?\)
- \(z\)
The image of \(d\) is ?
- \(z\)
The domain of \(f\) is ?
- \(A\)
The codomain of \(f\) is ?
- \(B\)
The preimage of \(y\) is ?
- \(b\)
\(f(A) = ?\)
- \(\{y, z\}\)
The preimage of \(z\) is?
- \(\{a, c, d\}\)

This is an image, created by Graphviz’s dot.

Questions

If \(f: A \to B\) and \(S\) is a subset of \(A\), then

\[f(S) = \{f(s)~|~s \in S\}\]

\(f(\{a,b,c)\}\) is ?
- \(\{y,z\}\)
\(f(\{c,d)\}\) is ?
- \(\{z\}\)

This is an image, created by Graphviz’s dot.

Injections

Injective: A function \(f\) from \(A\) to \(B\) is one-to-one or injective if and only if \(f(a)=f(b)\) implies that \(a=b\) for all \(a\) and \(b\) in \(A\) (the domain of \(f\)).

This is an image, created by Graphviz’s dot.

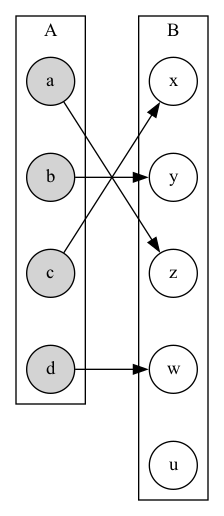
Surjection

Surjective: A function \(f\) from \(A\) to \(B\) is onto or surjective if and only if for every element \(b \in B\) there is an element \(a \in A\) such that \(f(x) = y\).

This is an image, created by Graphviz’s dot.

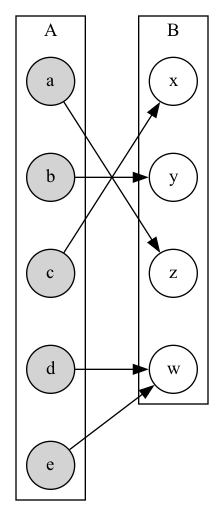
Bijection

Bijection: A function \(f\) from \(A\) to \(B\) is a one-to-one correspondence or a bijection if it is both one-to-one and onto (injective and surjective).

This is an image, created by Graphviz’s dot.

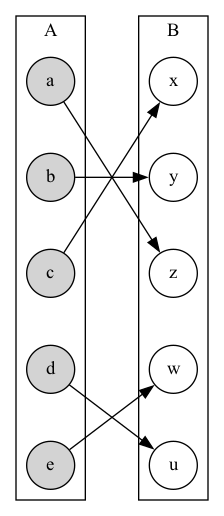
Proving injections and surjections

Suppose \(f: A \to B\).

To show \(f\) is injective:
- Show that if \(f(x)=f(y)\) for arbitrary \(x,y \in A\), then \(x=y\).

To show \(f\) is not injective:
- Find particular elements \(x,y \in A\), such that \(x \neq y\) and \(f(x)=f(y)\).

To show \(f\) is surjective:
- Consider an arbitrary element \(y \in B\) and find an element \(x \in A\) such that \(f(x) = y\).

To show \(f\) is not surjective:
- Find a particular element \(y \in B\), such that \(f(x) \neq y\) for all \(x \in A\).

Examples

Example 1: Let \(f\) be the function from \(\{a,b,c,d\}\) to \(\{1,2,3\}\) defined by \(f(a)=3, f(b)=2, f(c)=1, \text{ and } f(d)=3\). Is \(f\) surjective?

Solution: Yes, \(f\) is surjective since all three elements of the codomain are images of elements in the domain. What if the codomain was \(\{1,2,3,4\}\)?

Example 2: Is the function \(f(x)=x^2\) from the set of integers to the set of integers surjective?

Solution: No, \(f\) is not surjective because (for example) there is no integer x with \(x^2 = -1\).

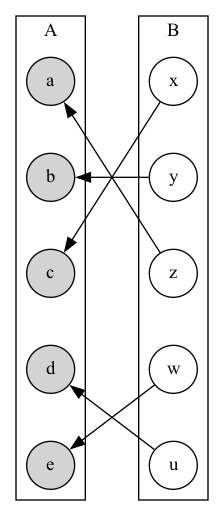
Inverse functions

Inverse: Let \(f\) be a bijection from \(A\) to \(B\). Then the inverse of \(f\), written \(f^{-1}\), is the function from \(B\) to \(A\) defined as \[f^{-1}(y) = x \text{ iff } f(x) = y\]

Non-bijective functions do not have inverses. Why?

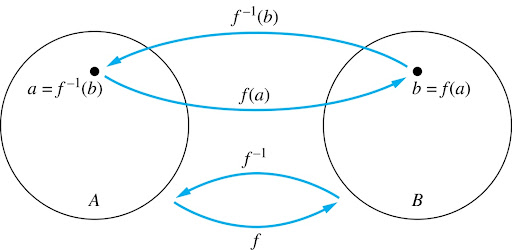
Inverse functions

\[f: A \to B\]

This is an image, created by Graphviz’s dot.

\[f^{-1}: B \to A\]

This is an image, created by Graphviz’s dot.

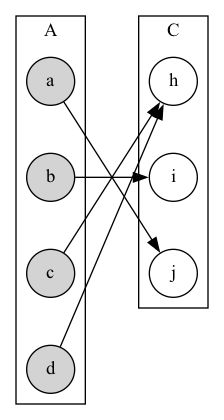
Composition

Composition: Let \(f: B \to C, g: A \to B\). The composition of \(f\) with \(g\), written \(f \circ g\), is the function from \(A\) to \(C\) defined by \[f \circ g(x) = f(g(x))\]

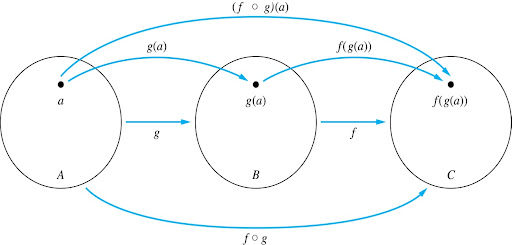
Composition

\[g: A \to B, f : B \to C\]

This is an image, created by Graphviz’s dot.

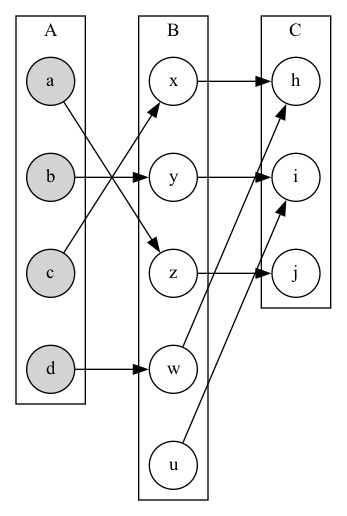
\[f \circ g: A \to C\]

This is an image, created by Graphviz’s dot.

Ceiling and floor

The floor of a real number \(x\), written \(\lfloor x \rfloor\), is the largest integer less than or equal to \(x\).
The ceiling of a real number \(x\), written \(\lceil x \rceil\), is the smallest integer greater than or equal to \(x\).

Examples

\(\lceil 3.5 \rceil = 4\)
\(\lfloor 3.5 \rfloor= 3\)
\(\lceil -1.5 \rceil = -1\)
\(\lfloor -1.5 \rfloor= -2\)